Introduction
When discussing glider designs whether indoor or outdoor, Hand Launch Gliders (HLG) or Catapult Launch Gliders (CLG) the subject of wash-out is typically brought up. Washout is typically thought of as twisting, shaping/sanding or adding an up tab to the trailing edge of the tips of a wing, so wing tips are at a negative angle of attack compared to the root of the wing. It is believed wash-out is desirable because its thought the tips stall first and putting the tips negative compare to the rest of the wing prevents this for happening. One can view the typically Lift Coefficient vs. Angle of Attack graph to understand why this theory is believed true. Also, it is important that both wingtips are wash-out equally otherwise a roll or aileron effect is created. Yaw makes the wash-out issues even more complicated, so to keep things simple the assumption of the wing flying level, no yaw is made.
Currently there are two methods typically used in glider designs to add wash-out to a wing. One is the typical way of shaping/sanding the wingtips. The other is to cut the dihedral joint skew to the centerline of the wing.
Typical Wash-out Method
For year’s wash-out appeared in many glider designs. Bending or sanding the wingtips at the trailing edge up about 1/16”, added wash-out. This was thought to improve the glide of the model along with the transition from launch velocities to glide velocities. The disadvantages of wash-out are added drag, and the possible added roll to the model. Bending tabs on any flying surface is thought to be very velocity dependent. This means the characteristics of the model will change dramatically with velocity. Since gliders go through a large range of velocities this is thought to be a concern. Also at high velocities the concern of the up tab bending or flexing is an issue. When parts of a glider flex /bend or the model is velocity dependent, the trimming of the model becomes very difficult.
To quantify the wash-out using this typical washout method it was decided that the change in angle of attack is the parameter of most interest. To calculate this change in angle of attack some trigonometry was applied.
The tangent function is defined as:
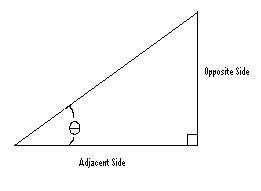
To calculate the wash-out in terms of angle of attack, set a reference line that passes thru the front point of the leading edge and trailing edge of the normal airfoil. Then set a line that passes thru the front point of the leading edge and trailing edge where the trailing edge has washed up. Calculate the angle between these two lines.

Tan=height washed up (H)/wing chord at this location(Wc)
Or
q = Arctan(H/Wc)
The following dimensions are taken from Super Sweep plans. To get an average angle of attack the dimensions were taken at the midpoint between the dihedral joint and the end of the wing.
Up tab = 1/16”
Wing Chord at wingtip locations = 2 “
Therefore the change in angle of attack is: q=Arctan(.0625/2)
or doing the math q=1.79 0
Now this is an approximation since wings are typically tapered or some other interesting elliptical shape. The angle of attack typically decreases as you move to the tip of the wing; this is not a constant number using the typical washout method. Still an approximation is better than nothing and some numbers are needed so intelligent design choices can be made.
The Dihedral Wash-out Method
Recently, the last 30 years, many glider designs cut the dihedral joint (poly-dihedral designs, outer dihedral joints only) skew to the centerline of the wing. Ron Whitman’s Super Sweep model had this feature, but its unknown whether he originated this idea.** After spending many hours talking to some great modelers about this subject it been concluded cutting the dihedral skew to the centerline of the wing can add wash-out or wash-in.
** I recently received correspondence from Lee Hines. He informed me that he used the dihedral joint method of glider washout technique in the early 1950’s. He believes to be the originator of the technique. (Update as of May 2007.)
Some paper models best illustrate the concept.
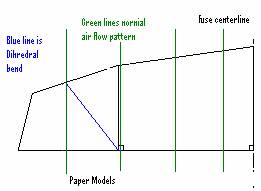
Take two pieces of paper, which is stiff enough to hold some shape. With a pen put lines on the paper, which is parallel to the centerline of the wing/fuse. This is basically the way the air flows across the wing when the wing is flying level and there is no yaw (This assumes a 2D model with no circulation around the wingtips). With one piece, bend in dihedral with the dihedral joint parallel to the centerline of the wing, the second piece put a skew angle outward (45 degrees). Now lay these pieces of paper on a flat board and measure the height from the paper to the board at both the leading and trailing at each of the pen lines. Since the paper is lying flat on the board these measurements are 0 for both the leading and trailing edge until you get to the dihedral joint. Then note what happens. For the one with the dihedral joint that is parallel to the centerline of the wing/fuse, the height changes as you measure to the tip but the height of the trailing edge and leading edge are equal at each pen line. The angle of attack of the wingtip has not changed compared to the rest of the wing. Now measure the one with the dihedral joint pointing outward, like the Super Sweep design. After the dihedral joint the leading edge height is smaller than the trailing edge height at a specific pen line, essentially putting the tip negative compared to the rest of the wing. From this it can be concluded the wing has been wash-out.
The advantages of adding wash-out by this method is it eliminates many of the disadvantages mentioned with adding wash-out the typical way. The disadvantage of wash-out using this method is that the whole tip is at the same angle of attack, where with the typically wash-out method the angle of attack decrease as you move out further on the tip.
Again to quantify the wash-out using this dihedral wash-out method it been decided that the change in angle of attack is the parameter of most interest. To calculate this change in angle of attack you need to apply some trigonometry.
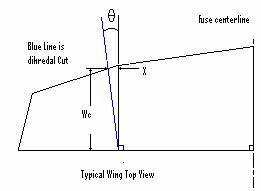
Most plans do not give the angle just the Distance off of the dihedral joint, which is parallel to the centerline of the wing (X).
Tan q=[Distance off of the dihedral joint (X)]/[Wing Chord(Wc)]
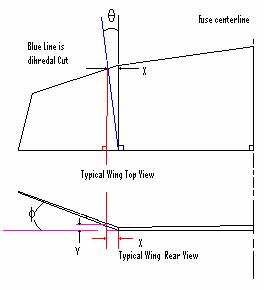
Now, Tan f =Y/X Where f is equal to the dihedral angle
Substituting in for X where X= Tan q* Wc and solving for Y the following equation is derived: Y=Tan f*(Tan q * Wc)
Now to calculate the angle of attack
Tan Y = Y/Wc
Substitute in for Y; Y=Tan f*(Tan q * Wc)
and Solving for Y
Y=Arctan (Tan f*Tan q)
Again the following dimensions are taken from Super Sweep plans
X =1/16”
Wing Chord (Wc)= 2.945 “
Dihedral angle = 17 degrees (1.25” high tip)
The skew angle for the dihedral cut is
Tan q =.0625/2.945 = .02122
Therefore the change in angle of attack is:
Y=Arctan (Tan 17*.02122) or doing the math Y=.37 0
Conclusions
The issue whether a good glider design should have wash-out in a wing is still not understood or settled. What is clear is there are at least two ways to create wash-out in a wing. The two methods were described both offer some advantages and disadvantages.

